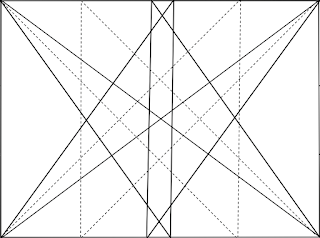
Expanded Dynamic Symmetry Armature
We will construct an expanded dynamic symmetry armature to include the diagonals, their reciprocals and rebated squares. These elements have been used by artists throughout history.
We begin with main diagonals and one reciprocal. We call the intersection of the diagonal with its reciprocal a polar point. Recall that a reciprocal is perpendicular to a diagonal by definition or they meet at 90 degrees. We drop a vertical line from the intersection of the reciprocal with the top edge to the bottom edge.
We shall prove that the vertical rectangle created with this dropped vertical as the left edge has the same aspect ratio as the main rectangle.
First the triangles formed by the reciprocal and diagonal are marked with angle a and angle b as indicated.
From Euclidean geometry we see that angle a plus angle b + 90 = 180 degrees. And angle a plus angle b = 90 degrees. Note the upper right corner is a 90 degree angle. Therefore the two component angles add up to 90 degrees and we again see angle a plus angle b = 90 degrees at the corner. Then the angle in the lower right corner must also be equal to angle b since the other two angles in the lower right triangle are 90 and angle a. Also, the lower left corner of the rectangle has an angle equal to angle b, this time using the full lower right corner as a 90 angle.
We label the corners of the rectangle A, B, C and D as indicated and the intersections of the vertical with the edges E and F:
Then the (larger, half-rectangle) triangle BCD (with angles a, b and 90 degrees) has the same angle measurements as the (smaller, half vertical rectangle) triangle EBC. They are said to be similar.
From Euclidean geometry two similar triangles have their sides in proportion. This means that BD:BC is the same proportion as BC:EB. Finally, rectangles ABCD and the vertical Rectangle BCFE have the same aspect ratio.
Visually, if we rotate the smaller vertical rectangle BCFE about its polar point 90 degrees, its diagonal will lie on the main diagonal. So we see visually again what we have just proven.
We construct the same lines on the left side to get the Expanded Similar Rectangles Armature (without labels now):
Note how this armature is different from the Basic Armature.
Now we construct the Rebated Squares Armature:
Construct the dotted square with its dotted diagonals on the left, with the sides all the same size as the larger rectangle's shortest side. This is called rebatement of the rectangle; the shorter side is rotated about the longer side.
Then complete both sides.
Rebatement of the rectangle was popular for many artists.
And finally, combine the two:

Expanded Dynamic Symmetry Armature
These diagonals create motion and the artist will try to align elements of the scene with these diagonals when possible. Also align vertical elements with the lines.
Note that from each corner, 3 lines emanate to other vertical endpoints or corners.
The nationally known artist, Michele Byrne, utilizes this armature in her paintings, drawing it on panels before painting. She reports that her audience noted that her compositions improved once she began using these armatures.
.